Does a brain-inspired network finally connect Transformers to true reasoning?

The Dragon Hatchling: The Missing Link between the Transformer and Models of the Brain

Since the 1940s, artificial intelligence and neuroscience have shared a fundamental mystery: how does intelligence actually work? From von Neumann and Turing to today’s researchers, the dream has been to bridge the gap between artificial language models and biological neural networks. Current AI systems like GPT face a critical limitation - they don’t generalize chain-of-thought reasoning beyond scenarios seen during training.

This challenge runs deeper than performance metrics. The brain operates as a distributed system with 80 billion neurons and over 100 trillion synapses, using local interactions and plasticity. Modern transformers rely on dense matrix operations and global attention mechanisms. The two approaches seem fundamentally incompatible, leaving us with artificial systems that lack the adaptability and interpretability of biological intelligence.

Figure 1: The Dragon Hatchling acts as a bridge between Transformer architectures and brain models, defining inference mechanisms both at the vector level and through particle dynamics of neurons and synapses.

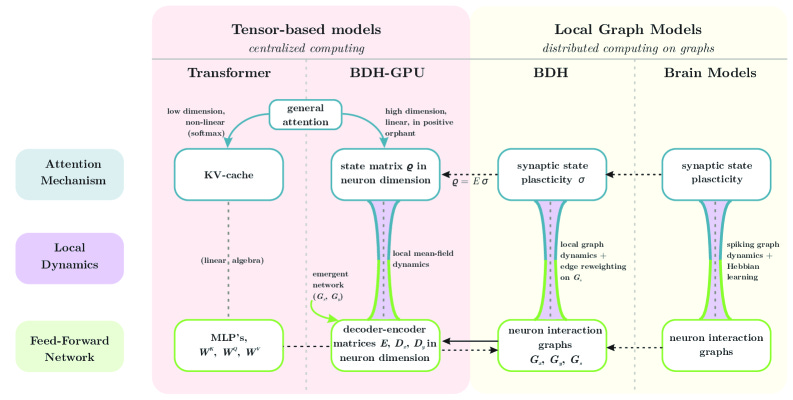
Researchers have now introduced Dragon Hatchling (BDH), a revolutionary architecture that bridges this gap. BDH combines strong theoretical foundations with inherent interpretability while matching Transformer-like performance. Unlike traditional neural networks, BDH operates as a scale-free, biologically-inspired network of locally-interacting neuron particles.

The breakthrough lies in BDH’s dual nature - it functions both as a practical GPU-trainable language model and as a biologically plausible brain model. The working memory relies entirely on synaptic plasticity with Hebbian learning using spiking neurons. Individual synapses strengthen when the system processes specific concepts, creating direct correspondences between artificial and biological mechanisms.

Combining Logic with Learning

The Dragon Hatchling’s foundation rests on merging two fundamental principles: logical inference and biological learning. The system implements modus ponens reasoning - if fact i is true and rule σ indicates i implies j, then j becomes true. In approximate reasoning, this translates to weighted beliefs where the strength of implication σ(i,j) determines how belief in i contributes to belief in j.

Hebbian learning provides the adaptive component. Following the principle “neurons that fire together wire together,” synaptic connections strengthen when one neuron’s activity leads to another’s firing. The system increases the significance of implication σ(i,j) whenever fact i contributes evidence for j during operation.

This creates a reasoning system with two types of rules: fixed parameters G learned through training (like traditional model weights), and evolving rules σ that adapt during inference (fast weights). The 1:1 ratio between trainable parameters and state variables proves crucial for practical reasoning systems, explaining the success of both Transformers and state-space models.

The graph-based formulation emerges naturally. With n facts and m = O(n²) potential connections, sparsity constraints create n ≪ m ≪ n² relationships. This produces graph interpretations with n nodes and m edges, where edges carry both state and trainable parameters while mediating communication between nodes.

Technical Contributions

The research introduces three major innovations bridging artificial and biological intelligence. First, BDH represents all model parameters as topology and weights of communication graphs, with state during inference represented as edge-reweighting applied to graph topology. This creates a programmable interacting particle system where particles act as graph nodes and scalar state variables reside on edges.

Figure 2: BDH as an oscillator network with particles connected by elastic connectors representing synaptic state.

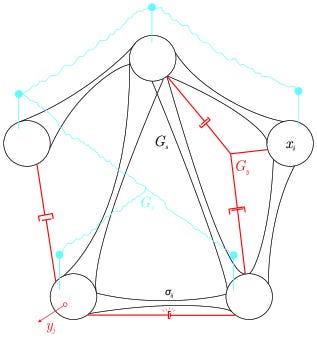
The local kernel naturally maps to graph-based spiking neural networks with Hebbian learning dynamics, excitatory circuits, and inhibitory circuits. This biological correspondence isn’t superficial - it captures the actual computational mechanisms needed for language processing and reasoning.

Second, BDH-GPU provides a tensor-friendly implementation through mean-field approximation. Rather than explicit graph communication, particles interact through “radio broadcast,” enabling efficient GPU training while maintaining mathematical equivalence to the graph model. The system scales primarily in a single neuronal dimension n, with three parameter matrices E, Dx, Dy containing (3+o(1))nd parameters.

Third, empirical validation demonstrates Transformer-level performance. BDH rivals GPT-2 on language and translation tasks with identical parameter counts (10M to 1B parameters) using the same training data. The architecture exhibits proper scaling laws while providing unprecedented interpretability through its biological correspondence.

From Graph Dynamics to Neural Networks

BDH operates through local distributed graph dynamics rather than global matrix operations. The system consists of n neuron particles communicating via weighted graph topology, with inference dynamics governed by edge-reweighting processes called the “equations of reasoning.”

The mathematical formulation centers on interaction kernels with programmable rulesets. For a system with z species and state (q₁,...,qz), transition rates determine how species interact: qₖ’ := (1-dₖ)qₖ + Σᵢⱼ rᵢⱼₖqᵢqⱼ. This general form restricts to edge-reweighting kernels suitable for distributed implementation while remaining expressive enough for attention-based language models.

The scheduler executes kernels in round-robin fashion, with each round involving local computation at neuron nodes followed by communication over wire connections. State variables X(i), Y(i), A(i) represent rapid pulse dynamics at neurons, while σ(i,j) captures synaptic plasticity between connected pairs.

Understanding Attention as Micro-Logic

Traditional attention mechanisms operate at the vector level through key-query-value transformations. BDH reveals attention’s micro-foundational structure as logical inference between individual neurons. Each attention state entry σ(i,j) represents an inductive bias - how likely the system considers implication i→j when proposing next conclusions.

The interpretation follows logical axioms: if past context implies implication i→j has weight σₜ₋₁(i,j), and current state implies i follows with weight xₜ(i), then j follows with weight xₜ(i)σₜ₋₁(i,j). This resembles the logical axiom (X→(i→j))→((X→i)→(X→j)), fundamental across different formalizations of logic.

Unlike traditional attention’s key-query lookup intuition, BDH’s micro-interpretation shows that σ(i,j) doesn’t represent logical truth values but utility-based inductive biases. These guide inference processes from known concepts to intermediate concepts likely serving as logical shortcuts between source and target concepts.

Chains of implications guide activations along paths in system graphs. Attention allows specific implications to enter reasoning paths once corresponding synapses open in state σ. This creates a reasoning system that heuristically evaluates which facts appear most plausible for next evaluation, following what resembles informal reasoning in language.

Research in biologically-plausible brain graph transformers has explored similar micro-level interpretations of attention mechanisms, providing complementary evidence for attention’s role in biological neural processing.

The Physical Model: Neurons as Oscillating Particles

BDH admits interpretation as a physical dynamical system of interacting particles. The toy-model places n particles in a circle connected by elastic connectors representing synaptic state σ(i,j). The system exhibits dual-timescale dynamics: slow tension evolution on connectors and rapid pulse activation at nodes.

Figure 3: BDH-GPU scales linearly in dimension n with fixed parameters d, k (neuron pairing), and h (attention heads)

Elastic connectors initially have zero displacement. When pulse displacement x(i) occurs at node i, accumulated tension from adjacent connectors σ(i,·) activates prods Gy, perturbing connected nodes. Sufficiently strong perturbation causes activation y(j) at node j, which propagates through wires Gx to modify pulse displacements x(i’) at other nodes.

The key mechanism: temporal correlation between pulse y(j’) followed immediately by pulse x(i’) increases tension σ(i’,j’) on the corresponding connector, even without direct causality. This captures Hebbian learning where coincident activity strengthens connections.

From connectors’ perspective, existing tension σ(i,k) propagates through prods to nodes j, then through wires to nodes i’, finally contributing to tensions σ(i’,j’) on other connectors. This creates three-hop propagation through i→j→i’, enabling complex state evolution supporting reasoning and memory.

From Brain Models to GPU Implementation

The transition from BDH’s biological formulation to BDH-GPU’s practical implementation maintains mathematical equivalence while enabling efficient training. BDH-GPU treats the n-particle system through mean-field interactions rather than explicit graph communication.

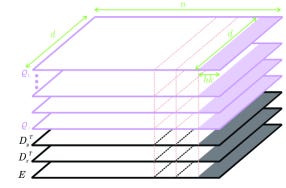
Each particle i maintains state ρᵢ(t) consisting of vectors in Rᵈ for each layer. Particle interaction depends on tuple Zᵢ containing current state, encoder E(i,·), and decoders Dx(·,i), Dy(·,i). The system scales uniformly in dimension n, bound into k-tuples when using block-diagonal matrices like RoPE (k=2) or ALiBi (k=1).

Figure 4: Neuron-neuron communication through graph H with m edges creates interaction graph G = H² enabling signal propagation Gz = H²z

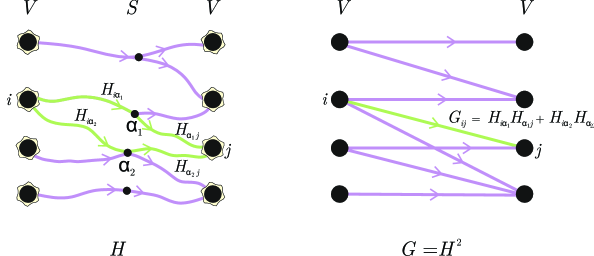
The interaction follows broadcast communication: each particle computes message mᵢ ∈ Rᵈ locally, broadcasts to receive mean-field message m̄ = Σⱼmⱼ, then updates local activation and state based on the broadcast result. This eliminates communication bottlenecks while preserving the essential particle dynamics.

From an engineering perspective, transformations between length-n vectors pass through intermediary dimension d representations. The encoder E reduces n-dimensional vectors to d dimensions before decoders Dx, Dy lift back to n dimensions. This low-rank factorization maintains O(nd) parameters while enabling high-dimensional reasoning.

Performance Results: Matching GPT-2 While Being Interpretable

BDH-GPU demonstrates competitive performance across language and translation tasks. The architecture retains Transformer advantages including parallel trainability, attention mechanisms, and scaling laws while adding biological interpretability and novel capabilities.

Figure 5: Single layer of BDH-GPU with inputs/outputs xl-1,yl-1 ∈ Rⁿ, parameters E ∈ Rⁿˣᵈ and Dx,Dy ∈ Rᵈˣⁿ shared across layers, and persistent state ρl ∈ Rⁿˣᵈ

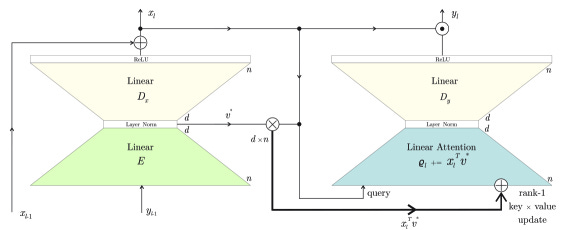
Architecture differences from GPT-2 include fewer parameter matrices enabling compact interpretation, scaling almost exclusively in neuronal dimension n, matching key-value state and parameter matrix dimensions, no context length limits, linear attention in high dimensions, and positive sparse activation vectors.

Figure 6: BDH-GPU matches GPT-2 performance across model sizes on translation tasks, with simpler scaling properties requiring only variation in neuron count n

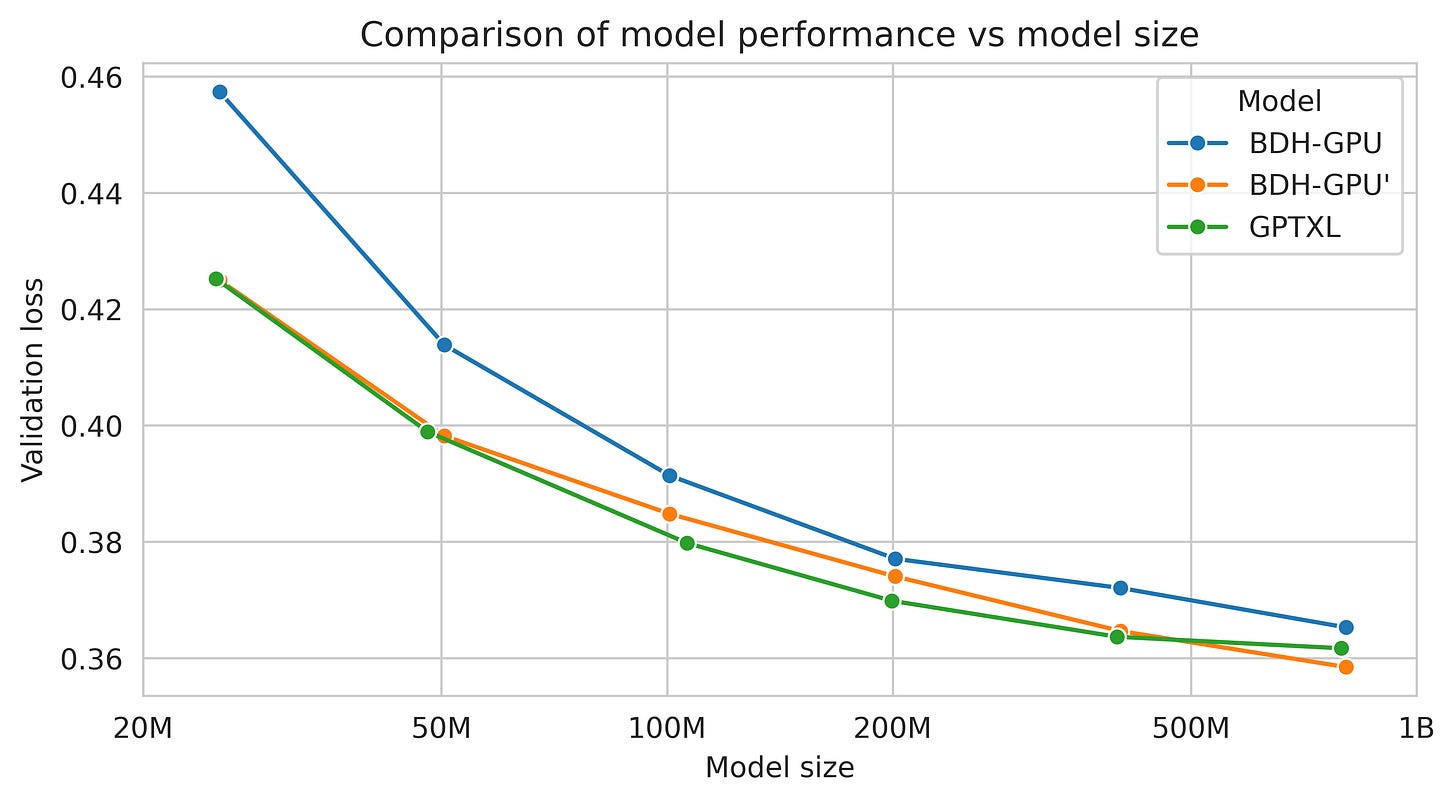
The scaling experiments demonstrate Transformer-like loss reduction with parameter count. BDH-GPU generally shows improved loss reduction per data token, learning faster than Transformers on both natural tasks like translation and synthetic puzzles requiring reasoning.

FLOPS counts during inference bound at O(ndL) operations per token. Each parameter accesses O(L) times per token with typical layer counts smaller than Transformers. State access requires O(1) operations per token with small constants. The simple implementation ignores activation sparsity opportunities, suggesting further efficiency gains.

Emergent Intelligence: How Structure Emerges Naturally

Large-scale reasoning systems benefit from hierarchical modular structure. Rather than designing modularity explicitly, BDH demonstrates how scale-free modular structure emerges naturally through local graph dynamics during training.

Graph systems serving information propagation functions tend to achieve modular structure optimizing efficiency-accuracy tradeoffs. This emergence offers advantages over explicit partitioning: nodes belong to multiple communities and act as bridges, scales and relationships between communities evolve dynamically as importance changes, and new connections emerge naturally.

The historical precedent appears in World Wide Web evolution from catalogue-based systems (DMOZ, Craigslist) to naturally evolving knowledge webs (Wikipedia), interlinked communities (Reddit), and network-structure-based expert weighting (Google PageRank). Newman modularity formalization and Stochastic Block Models provide theoretical frameworks for studying these phenomena.

Scale-free properties manifest system operation at criticality - sufficiently stable for short-term information retrieval yet adaptable enough for abrupt behavioral changes as new knowledge invalidates previous reasoning paths. The standard definition requires polynomial likelihood that new information affecting n’ nodes follows power-law distribution in 1/n’.

For most information propagation dynamics, this necessitates power-law degree distributions under uniformity assumptions. BDH exhibits these properties empirically, suggesting operation at criticality enabling both stability and adaptability in reasoning systems.

The ReLU-Lowrank Innovation

BDH-GPU’s ReLU-lowrank blocks capture different properties than typical low-rank approximations in machine learning. The blocks serve noise reduction and faithful representation of affinity functions on sparse positive vectors, making them suitable for Linear Attention combinations.

The ReLU-lowrank operation maps z ∈ Rⁿ to fDE(z) := (DEz)⁺ where encoder E transforms length-n vectors to length-d, decoder D transforms back, and ReLU ensures positive outputs. This differs from standard MLP blocks but provides comparable expressiveness for functions in positive orthants.

Figure 7: ReLU-lowrank feedforward networks enable community-based neuron activation, where neurons activate based on signals from their own communities

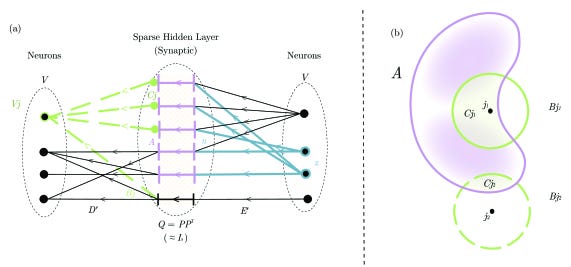
Error analysis shows low-rank approximation G ≈ DE achieves O(√(log n/d)) pointwise error for matrices with ‖G’‖₁,∞ ≤ 1. Adding ReLU suppresses noise, enabling closer approximation of positive transformations like Markov chain propagation z ↦ G’z for stochastic G’.