Can AI learn to prove theorems by thinking step-by-step like a human mathematician, even without perfect instructions?

Seed-Prover: Deep and Broad Reasoning for Automated Theorem Proving

Large language models show strong mathematical reasoning through reinforcement learning with long chain-of-thought approaches, yet they struggle with theorem proving due to the lack of clear supervision signals when using natural language alone. Verifying proofs in natural language proves extremely difficult - each step must be carefully checked for correctness, making automatic or even manual verification nearly impossible.

Recent work like AlphaProof demonstrates the power of formal verification by using Lean to solve 3 problems from the 2024 International Mathematical Olympiad (IMO). This success shows that LLMs using formal theorem proving approaches can tackle challenging problems that natural language approaches fail to solve. Unlike natural language, formal languages like Lean provide clear, automatic signals about proof correctness through formal verification.

Figure showing the progression of performance on MiniF2F-Test benchmark, demonstrating significant improvements over time with Seed-Prover achieving saturation.

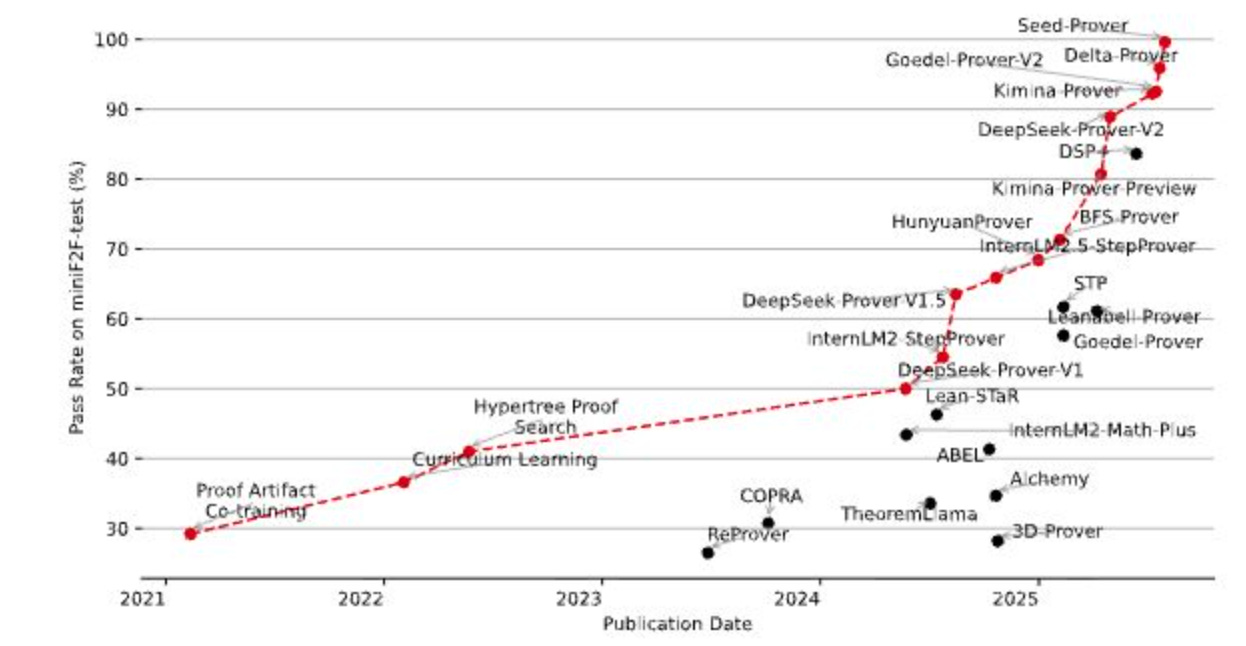
Introducing Seed-Prover: A New Paradigm

The research introduces Seed-Prover, a lemma-style whole-proof reasoning model that represents a significant departure from existing approaches. Current formal provers fall into two categories: step-level provers that incrementally generate Lean code line-by-line, and whole-proof models that generate complete proofs at once. Step-level provers enable close interaction with the Lean environment but require special scaffolding and often involve overly granular interactions that hinder high-level reasoning. Whole-proof models avoid these issues but typically lack interaction with the Lean compiler.

Seed-Prover combines the best of both approaches through four key innovations: